Zomergast Ionica Smeets, Wilfried de Jong, Fibonacci, Ananas, God

Ionica Smeets en Wilfried de Jong in Zomergasten 17 aug 2014

Een geslaagde zomeravond uitzending zondag 17 augustus 2014 met 'wiskundemeisje' en wetenschapsjournalist Ionica Smeets. Wilfried de Jong was de gastheer. Hij deed het erg goed. 

Ik haal er één item uit. Gezien mijn jarenlange bemoeienis met Darwin, evolutie en Intelligent Design, zal het U niet verbazen dat één opmerking van Wilfried de Jong bij mij insloeg als een bom. Het onderwerp: het aantal spiralen op een ananas die een Fibonacci reeks 1, 1, 2, 3, 5, 8, 13, 21, 34, ... vormen. Naar aanleiding daarvan merkte hij op:

"Dat zou je spontaan streng gelovig maken. Dat iemand dit heeft uitgedacht. Iemand nog veel ouder dan Fibonacci. Een 'Fibonacci op een wolk'! (...)
Want als de oerknal heeft plaatsgevonden, hoe kom je dan tot zulke precieze dingen?"

Een geweldige, onthullende, ontroerende opmerking. Heerlijk! Om van te smullen! Zeer waarschijnlijk is het een authentieke, spontane ingeving, maar wetenschappelijk naief. Naief, omdat het een variant is op de eeuwenoude, achterhaalde en niet uit te roeien vraag of het heelal ontworpen is. Toch begrijp ik de vraag wel. Voor een leek is het mysterieus dat een plant een wiskundige reeks kan maken. Wiskunde is door mensen uitgevonden. Wiskunde is moeilijk, het is iets voor nerds. Dus de ananas-ontwerper moet op z'n minst een geniale wiskundige zijn. Een begrijpelijke reactie van een niet-wetenschapper. Over het antwoord van Ionica straks meer. En op het eind laat ik zien dat de ontwerper-gedachte getypeerd wordt door inconsequent denken. Maar eerst wat nuanceringen.

Eerst wat nuanceringen

Toen Ionica de spiralen op een meegebrachte ananas liet zien, maakte Wilfried spontaan de (cruciale!) observatie dat die ananas "een kleine afwijking had. Het is een beetje gekke ananas. Sommige spiralen zijn wel een beetje moeilijk te zien". Inderdaad, ik heb thuis bij mijn eigen exemplaar geconstateerd dat er vaak 'een knik' zit in de spiraal. Er zijn dan wel 8 of 13 spiralen te tellen, de spiralen zelf zijn slordig gevormd [3]. Of het altijd Fibonacci getallen zijn, zou je toch wel 100 en liefst 1000 ananassen moeten scoren! Dat weet Ionica ook wel.

Wat is een afwijkende ananas? Bestaan er 'standaard' en 'afwijkende' ananassen? In de natuur is variatie de norm. Voor Darwin was variatie de basis van zijn evolutietheorie. Zelfs in een cultuurgewas als de ananas is variatie niet verdwenen. Als je het youtube filmpje van Vi Hart eens nauwkeuriger bekijkt, dan blijkt ze te zeggen:

"De drie groepen spiralen op elke ananas vormen bijna altijd een Fibonacci-reeks. Heel soms is het een Lucas-reeks, maar altijd drie getallen in een reeks."

Kijk! Dan worden de mogelijkheden al wat ruimer om patronen te herkennen. Is het niet de ene, dan is het wel de andere reeks. (De Lucas reeks verschilt van de Fibonacci reeks door de twee begingetallen).
Nog een noodzakelijke nuancering: de Fibonacci getallen reeks is oneindig lang. Dan zijn twee of drie getallen 8, 13, 21 wel een èrg magere afspiegeling van de oneindigheid. Het zijn bovendien ook nog kleine getallen. Fibonacci getallen worden oneindig groot. En tenslotte: de Fibonacci reeks wordt gevormd door simpele optelling van de twee voorgaande getallen. Eenvoudiger kan het niet. Hogere wiskunde als aftrekken, delen, kwadrateren, worteltrekken komt er niet aan te pas.

Realistisch?

Ik vond een terloopse, maar in dit verband cruciale, opmerking in het boek The Algorithmic Beauty of Plants [1]. Dat boek gaat over L-systemen. Dat zijn algoritmes uitgevonden door prof. Lindenmayer, waar ik ooit college bij gelopen heb (Utrecht). Die algoritmes genereren het systeem waarop bladeren aan de stengel van planten bevestigd zijn. Dit vond ik in het boek:

"Alternatively, random selection of similar surfaces could have been employed to prevent the excessive regulairty of the resulting image." (p. 104. [1])

Onthullend: excessive regulairty!  Om de planten realistisch te maken moet er een klein beetje random variatie aan de algoritmes toegevoegd worden! Anders zouden ze er als ... tsja, als computertekeningen uit zien!  

"Want als de oerknal heeft plaatsgevonden, hoe kom je dan tot zulke precieze dingen?" Antwoord: ze zijn minder precies dan je denkt. Planten zijn niet perfect mathematisch gevormd. Als planten door een computer gegenereerd worden, zie je onmiddellijk dat ze niet levens-echt zijn. Dit random aspect vind je ook terug in de meer geavanceerde recentere computer modellen van plantengroei [4].

Hoe moeilijk is Fibonacci te maken?

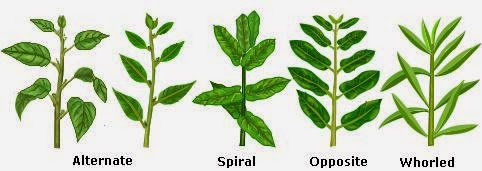
Hoe moeilijk is het eigenlijk voor een plant om een Fibonacci patroon te vormen? Er zijn planten waar opeenvolgende paren bladeren een hoek van 90 graden vormen (bijv.: de bekende kamerplant siernetel): is 90 graden moeilijker of makkelijker dan 137,5 graden? 

de belangrijkste 4 bladstanden (phyllotaxis).
Voor verklaring zie hier. De tweede is de siernetel

Of: is het makkelijker voor een menselijke embryo om precies 5 vingers aan iedere hand te maken? Of een hoofd met precies 2 ogen, 1 neus, 1 mond, en 2 oren in de juiste proporties en in de juiste posities op het hoofd? Ik denk dat Fibonacci patronen makkelijker zijn, juist omdat ze zo voorspelbaar, mechanistisch, deterministisch, ja, wiskundig zijn. Daarom kan de plant het met een voorgeprogrammeerd cellulair algoritme doen. Omdat er geen wiskundige formule is voor de constructie van het hoofd, nemen we aan dat een hoofd niet moeilijk te maken is. Maar dat hoeft natuurlijk niet zo te zijn.

Hoe kan een plant een Fibonacci reeks maken?

Ionica gaf als antwoord aan Wilfried de Jong: 

"Ik denk dat er wel een goede evolutionaire redenen is om op deze manier te groeien."

Nu, of er goede 'evolutionaire redenen' zijn, daar zijn de deskundigen het nog niet over eens. Als je het als een fitness probleem opvat, dus functioneel probleem, dan lijkt het op een optimalisatieprobleem. Bijvoorbeeld: hoe kun je met de minste lege tussenruimtes zoveel mogelijk zaden op een oppervlakte plaatsen? (dat is een wiskundig packing problem). Of: hoe kun je bladeren aan de stengel rangschikken met de minste schaduw voor onderliggende bladeren? (controversieel)
Als je kijkt naar directe oorzaken, dan vind je verschillende mechanismes en modellen in de wetenschappelijke literatuur. De ontwikkelingsbioloog Brian Goodwin heeft dit al 20 jaar geleden uiteengezet in zijn populair-wetenschappelijk boek How the Leopard Changed Its Spots (zie mijn review + speciale update n.a.v. de uitzending). 

phyllotaxis: om-en-om;  spiraal,  tegenover-elkaar;  krans

De Fibonacci spiraal verklaart Goodwin aan de hand van het fysische model van Douady and Couder die laten zien dat een Fibonacci patroon ontstaat wanneer je magnetische geladen druppeltjes in een schaaltje met een vloeibaar medium laat vallen. Het patroon ontstaat door onderling afstotende interacties van de druppels die zich vrij kunnen bewegen in het medium. Puur fysische krachten dus. Puur fysische krachten kunnen onder bepaalde condities Fibonacci patronen vormen. Goodwin suggereert dat cellen in een groeipunt van een plant zich op dezelfde manier gedragen. Het eindresultaat van het puur fysische mechanisme vertoont in ieder geval frappante overeenkomsten met het biologische mechanisme.

Richard Smith (2006) phyllotaxis model.
bij auxine maximum (rood) ontstaat nieuw orgaan
A: tweede orgaan gaat ontstaan, B: derde gaat ontstaan

Een recente publicatie [2] (zie plaatje hierboven) beargumenteert de centrale rol van de distributie van het plantenhormoon auxine over cellen van een groeipunt. Naburige cellen remmen elkaar. Een lokaal maximum van auxine veroorzaakt een nieuw orgaan. Wordt de onderlinge afstand groter dan is de remmende invloed kleiner, en kunnen nieuwe cellen/organen ontstaan. Het Fibonacci-patroon is niet van te voren in miniatuur aanwezig, maar ontstaat tijdens het groeiproces. Dit model kan getest worden met auxine-remmers. Er zijn additionele factoren betrokken die het patroon stabiliseren en er zijn mutanten. Mutanten zijn belangrijk: zegt iets over de genen die het aansturen.
Het grappige dat dit model ook weer een computer model is dat zowel rekent als 3-D plaatjes tekent, en uiteindelijk Fibonacci patronen produceert. En een hoop andere phyllotaxis patronen afhankelijk van de condities.

Het beste antwoord

Een 'Fibonacci op een wolk' is het antwoord van een dominee. Een dominee verklaart een regenboog met God, niet met Newton. Het antwoord van een wetenschapper is dat 'Ontwerper' als verklaring al eeuwen geleden uit de wetenschap is verdwenen. Zelfs als we geen volledig wetenschappelijk verklaring hebben, is de God-theorie wetenschappelijk onacceptabel, overbodig, ad hoc. Het heeft geen voorspellend vermogen, en het frustreert wetenschappelijke onderzoek. Het is niet eens een theorie. 

Toegift voor de wiskundige ananasliefhebber

fout: symmetrisch

fout (idem)

te vierkant

Op het internet vind je veel 'foute' ananassen. Fout volgens de wiskunde (volgens Ionica). De eerste twee zijn symmetrisch, de derde is niet symmetrisch maar de 'cellen' zijn nogal vierkant. De makers van het kinderprogramma Spongebob hadden het kennelijk ook niet begrepen, want een ananas heeft géén bilaterale symmetrie (volgens Vi Hart).

Toen ik onderstaande plaatje tegenkwam in het boek van Philip Ball The Self-made Tapestry, moest ik onmiddellijk denken aan de ananas. Zó zou de ananas er ideaal gesproken uit moeten zien!

 

Géén ananas! maar hexagonale cellen in een vloeistof (bron)

De werkelijkheid is iets anders:

een echte ananas: slordige zeshoeken...

deze komt aardig in de buurt van zeshoekige cellen...

Vraag voor de wiskundige ananasliefhebber: moeten volgens wiskundige principes de 'cellen' van de ananas zeshoekig zijn om spiralen te kunnen vormen? of kunnen het ook vierkanten of driehoeken of ... zijn? Werd niet verteld in de uitzending.

links: veel ruimte, rechts: weinig tussenruimte (bron)
hexagonaal i.p.v. cirkels heeft geen tussenruimte!

En: schrijft de wiskunde een specifieke hoek voor die spiralen moeten maken? En wat is de invloed van de vorm van de ananas op de spiralen? Dat zal samenhangen met de vorm van de cellen (bloemen).

Hier zie ik een paar enigszins evenwijdige verticale lijnen.
Overgangsvorm naar echte spiralen? (bron)

Overbekend hexagonaal patroon. Zowel verticale lijnen als
Rechtse en Linkse diagonalen zijn te zien. Is dit de ideale ananas???

Probleempje 

Het bovenstaand hexagonaal patroon heeft schuine naar links en rechts hellende lijnen, maar ook verticale rijen (6 stuks). De schuine lijnen lopen evenwijdig. Maar vouw je het patroon tot een cilinder, dan krijg je naar links en rechts draaiende spiralen. Dan heb je volgens mij een ideale wiskundige ananas. Maar er is een probleem. Het zou wel eens zo kunnen zijn dat je bij symmetrische patronen zoals bovenstaand altijd evenveel R- als L-draaiende spiralen hebt. Biologisch is daar niks mis mee, maar dan zijn het géén Fibonacci spiralen, want die moeten bijv. 8L en 13R spiralen hebben. Is dat de reden dat Ionica en Vi Hart zo met stelligheid beweren dat symmetrische ananassen geen Fibonacci-ananassen kunnen zijn? Maar kunnen ananassen dan wel hexagonale cellen hebben? Zo niet, wat is de vorm van de cellen dan wel? Wie kan hierover uitsluitsel geven?

Ondertussen vond ik dit schema van Hans Bär:

Wat duidelijk wordt is dat er op de linker 'spiraal' 8 cellen en op de rechter spiraal 5 cellen geplaatst kunnen worden. De linker spiraal heeft een kleinere hellingshoek (welke?), waardoor er meer cellen op geplaatst kunnen worden. Waarom hij overlappende driehoeken gebruikt is mij niet duidelijk (dennenappel?). Dat werkt in ieder geval niet voor de ananas omdat je op die manier geen goede vlakvulling krijgt. Wel wordt duidelijk uit deze figuur dat er geen bilaterale symmetrievlak kan zijn met verschillende hellingshoeken. Grappig dat hij de cellen in een rechte lijn heeft getekend! (vergelijk met mijn hexagon figuur!). De weergave van 0 tot 360° is ook aardig gedaan.

Toegift: het inconsequente 'ontwerper-denken'

Stel dat er een Ontwerper van het heelal zou zijn, waarom zou die Ontwerper uitgerekend een ananas en niet de mens uitgekozen hebben om wiskundig te ontwerpen? Is een ananas belangrijker dan de mens? Hmmm. Kun je überhaupt van een cultuurgewas, dat al 6000 tot 9000 jaar gekweekt en geselecteerd wordt door mensen, zeggen dat het door God geschapen is? Hmmm. En als er een geheime boodschap in verborgen zit ("the fingerprint of God"), hoeveel mensen zullen spontaan Fibonacci in een ananas herkennen? Helaas: Fibonacci zelf kan de ananas niet gekend hebben, want de de ananas kwam pas ná 1493 naar Europa. Jammer voor Fibonacci. Dus niemand vóór Fibonacci (1170 - 1250) kan de reeks herkend hebben. Trouwens, het Bijbelboek 'Genesis' rept niet over de Fibonacci-reeks. Maar goed, je kunt je er altijd uit redden met: Gods wegen zijn ondoorgrondelijk. 

Iemand heeft dit uitgedacht:

Icosahedral Capsid Protein van een virus (ViralZone)
de classificatie van virussen is op geometrische figuren gebaseerd!

Ik weet nog iets dat perfect mathematisch is ontworpen: virussen! Virussen zijn Regelmatige veelvlakken (Platonic solid). Er bestaan vijf regelmatige veelvlakken, die al bekend waren bij de Griekse filosofen. Voorbeelden: het herpes virus heeft de vorm van icosahedron. Zou Wilfried de Jong bij het zien van deze geometrisch gevormde virussen ook spontaan uitroepen: Dat zou je spontaan streng gelovig maken. Dat iemand dit heeft uitgedacht ? 

Hoe plausibel is het dat de ananasplant en vele andere planten doelbewust volgens een wiskundige reeks ontworpen zijn? God zou een universum gemaakt hebben dat gebaseerd is op een wiskundige reeks van een mens (een wiskundige) in plaats van dat God het zelf uitgevonden zou hebben? Dus dan zou het de God-reeks moeten heten. Hoe plausibel is het gezien alle afwijkingen? En hoe selectief is de waarneming. Waarom heeft God de maiskolf niet spiraalvormig ontworpen, maar 'nette' evenwijdige rijen gegeven? Waarom zijn appels en bananen niet volgens Fibonacci ontworpen? Waarom bestaat een spinneweb niet uit Fibonacci spiralen? i.p.v. concentrische cirkels? 

Waarom heeft mais evenwijdige rijen en geen spiralen?

Is het hele idee falsifieerbaar? Dus: alles wat niet uit Fibonacci spiralen bestaat is niet ontworpen? Als je consequent denkt! En waarom de keuze voor Fibonacci? Waarom het heelal niet op priemgetallen baseren? Wie geeft het antwoord?
Voor Fibonacci-fans: dit zijn Fibonacci-tijden: 8:13 en 13:21 en 21:34 ! Vergezocht? Leuk? Onzin? Een 7-daagse week lijkt een universeel gegeven in alle culturen, maar 7 is géén Fibonacci getal! Vervelend. Maar het zit wel in de Lucas reeks! Dus toch ontworpen? Alles is toegestaan als het maar 'wiskundig' is? Is het toeval dat de mens 5 (Fibonacci getal!) vingers per hand heeft? Of heb je altijd tenminste twee (opeenvolgende) getallen nodig? Voor de liefhebbers is er een speciale wikipagina Fibonacci numbers in popular culture!

Intelligent Design

ID-ers en creationisten beweren dat je Fibonacci overal tegenkomt in de natuur! (google maar even). Ik had een merkwaardige ervaring met de Amerikaanse ID-er en wiskundige William Dembski. Hij had de moed of brutaliteit om een criterium op te stellen waaraan je 'design' in de natuur kunt vaststellen. Toen ik hem er op wees dat Fibonacci in het plantenrijk voorkwam en aan zijn design-criteria voldeed, was hij in verlegenheid gebracht. Zijn design-criterium moest verschijnselen met een natuurlijke verklaring er uit filteren. Hij kende het voorbeeld niet (!) en wilde het tegelijkertijd ontkennen en bevestigen. Ik had hem zogenaamd niet begrepen. Hier kun je het nalezen.
Maar Intelligent Design komt niet alleen in de christelijke wereld voor, ook de moslims hebben Fibonacci ontdekt: God's Design in all things. Een rammelde website: Michael Behe wordt David Behe genoemd en dat is nog het minste.

De hele uitzending Zomergasten is nu op youtube te vinden! 

 

Noten

1. P. Prusinkiewicz, Aristid Lindenmayer (1990). 'The Algorithmic Beauty of Plants'. (toen erg duur, nu als gratis pdf op internet)
2. Richard S. Smith et al  (2006) A plausible model of phyllotaxis, PNAS 2006.
3. Als de Ontwerper het aantal spiralen exact kan laten ontstaan, waarom zou hij dan ook niet perfect mathematisch gevormde spiralen kunnen laten ontstaan? 
4. Noise and Robustness in Phyllotaxis (2012): "... all organisms are affected by natural stochastic variability..."

Vorig blog over Ionica Smeets

Ionica Smeets geniale verdediging van de zuivere wiskunde 29 maart 2011

Zie ook

Is er orde in de natuur? blog 2 Feb 2015